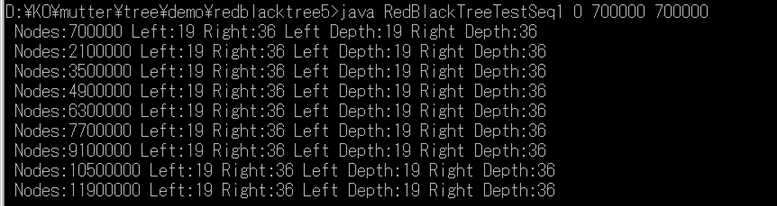
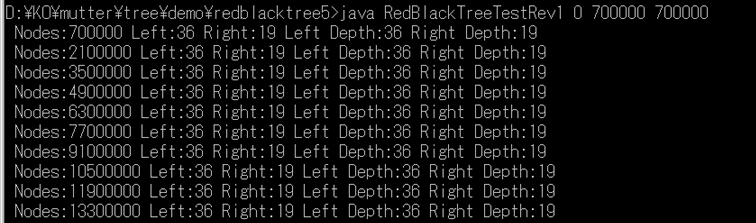
赤黒木 Red-Black tree
Javaの TreeMap が 使っている Red-Black tree を調べてみました。
2分探索木のノードに赤か黒の色をつけ、
以下の条件を満たしたものを 赤黒木 red-black tree といいます。
2色木とも呼ばれます。
- ノードは赤か黒である
- 根は黒である
- 全ての葉は黒である
- 赤いノードの子は黒である
- 全ての葉から根までのパスには、同じ個数の黒いノードがある
条件1、2、3、4から Red-Brack Tree に含まれる最短パスは黒ノードだけを含み、
最長パスには、赤黒が交互に含まれることになります。
最短パスと最長パスが(ざっくりといって)2倍をこえないようにバランスしている
というのが Red-Black Tree の特徴です。
全ノードに赤黒情報(1ビット)を追加し、
挿入・削除でバランスの崩れた箇所から、
最大3親等(挿入時は叔父まで、削除時は甥まで)のノードを調べ、
色を付け替えたり、
ローテーションしたりする操作を、
最悪根まで繰り返すことでバランスを保ちます。
Red-Black Tree の例
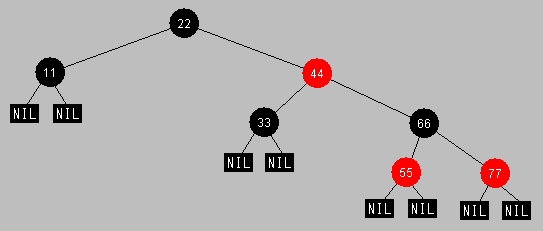
Red/Black Tree Demonstration で作図後 NIL を加筆
上図に 88 を挿入すると下図のようになります。
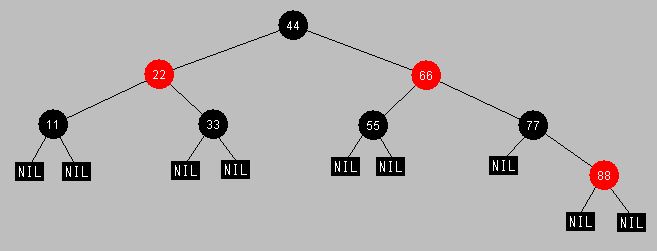
バランスしている2分探索木ですから、log(N)時間で検索されます。
挿入、削除については2分探索木に加えて、色の制約条件に合わせる操作が必要になりますが、
最悪、葉から根までの繰り返しで終了しますから、挿入、削除もlog(N)時間が保障されます。
条件3について実際のプログラムでは、葉が1つしかない場合や、葉にデータを持たせたり持たせなかったり
様々なバリエーションがあります。
ここではアルゴリズムが煩雑になるのを避けるために、データをもたない NIL という終端をあらわすノードを使い、
必ず左右の葉があることにします。
NIL は黒とします。
【検索アルゴリズム】
【挿入アルゴリズム】
2分探索木の挿入で要素を挿入し、
色を赤にします。
この後、近くのノードとの間で色の調整を行います。
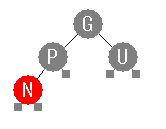 赤のノードを挿入したのですから、条件4に関する調整が必要です。
条件5を壊さないようにしながら、赤黒をつけかえるかローテーションするかします。
赤のノードを挿入したのですから、条件4に関する調整が必要です。
条件5を壊さないようにしながら、赤黒をつけかえるかローテーションするかします。
親の兄弟(親の親の子で、自分の親でない方)を叔父ノードと呼ぶことにします。
また、挿入されたノードを N 、 挿入時の N の親を P 、 親の親を G 、
叔父を U であらわします。
【挿入 ケース1】
N が根であれば、無条件に色を黒にできます。
条件のうち気になるのは条件5ですが、
赤が黒になって左右の両方のパスに対して黒の個数が1増えた状態で条件が守られています。
親 P が黒であれば条件4はOK。
N は赤で、自分の子は左右とも NIL(黒)であり、挿入した個所はもともとは NIL でしたから、
挿入によってパス上の黒ノードの個数は変わりません。よって条件5もOK。
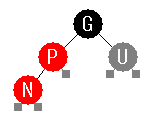
以上で親 P が黒の場合は終わりです。
問題は P が赤の場合です。
赤い P は根ではないので、G がいます。
G が赤とすると条件4により P は赤にはなりえないので G は黒だと判明します。
残っているのは、Uが赤の場合と黒の場合です。
【挿入 ケース2】
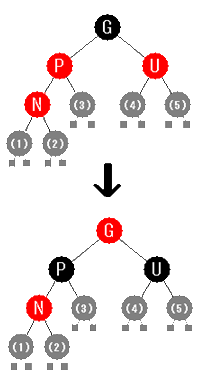
U が赤の場合。
G が黒であり、その下の階層( P と U )が2つとも赤ですから、
赤黒をいれかえ、G を赤に、 P と U を黒にしても
条件5はくずれません。
P と U が黒に変わったのですから条件4もクリアしています。
問題は G が赤になったことで、 G を新たな N として再帰的に色の調整を行います。
色の調整は最悪の場合、根まで伝播します。
残っているのは、U が黒の場合です。
G − P − N の色のパターンは、黒−赤−赤 ですから、
G と P と N の位置関係で4つの場合があります。
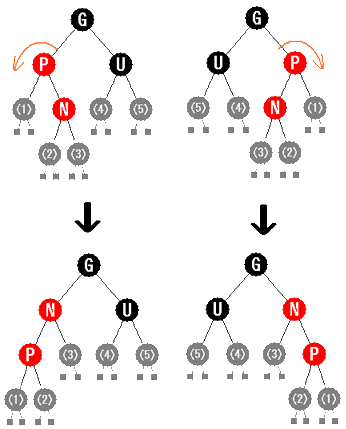
【挿入 ケース3】
G の左の子が P で、 P の右の子が N の場合と、
G の右の子が P で、 P の左の子が N の場合を考えます(右図)。
つまり部分木の内側の子として N がある場合は、
P を中心にして外側にローテーションすると、次のケース4に帰着できます。
(2) の部分木が N から P に付け替えられましたが、
親がいずれも赤ですから条件5は守られています。
P とか N は説明の便宜のためにつけた名前で、重要なことは赤か黒かです。
P と N を交換して(名前を付け替えて)、ケース4に進みます。
【挿入 ケース4】
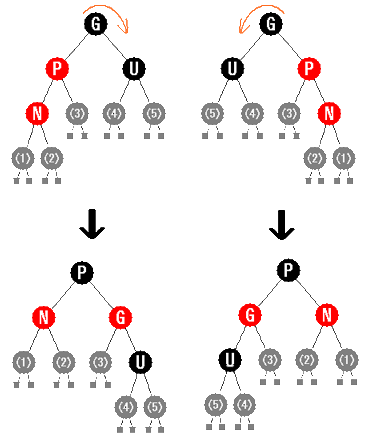
G の左の子が P で、 P の左の子が N の場合と、
G の右の子が P で、 P の右の子が N の場合を考えます(右図上)。
つまり N が部分木の外側の子である場合です。
まず、G を中心に内側にローテーションすると次のような状態になります。
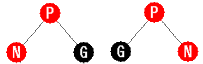
ここで、P (赤) と G (黒) の色を交換します(右図下)。
(3) の部分木が P から G に付け替えられましたが、
最終的には、赤から赤への付け替えですから、条件5は守られています。
ケース2以外はバランスの調整は完了です。
ケース2は G を挿入ノードとして再帰的に上位と調整します。
最悪でも根まで伝播しケース1で終了します。
【削除アルゴリズム】
2分探索木の削除は、削除したいノードを検索し、
- ノードに子がなければ、黙って削除する。
- 部分木が片方しかなければ、その部分木を昇格させる。
- 子が2ついたら、左部分木の最大値または右部分木の最小値をさがし、
自ノードの値とする。
値をもらったノードを(部分木の最大値または最小値なので、
子の数は 0 か 1 だから)上記 1. または 2. で削除する。
でした。最終的には、子の数が 1 以下のノードの削除に帰着しています。
赤黒のバランスも、このケース(自ノードが自分の唯一の子に置き換えられるケース)について考察すればよいことが判ります。
【削除 ケース0】
自ノードが赤の場合はバランスの調整は不要です。
赤が黒で置き換えられても 条件4、5に違反しないからです。
また、自ノードが黒で、子ノードが赤の場合は、置き換えと同時に赤から黒へ変更することで、
条件をまもることができます。
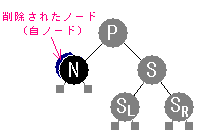 以下、削除される自ノードと、自ノードの後をつぐ唯一の子の両方が黒の場合について考察します。
削除によって、この部分の黒の段数が1減るため、バランスの調整が必要となります。
以下、削除される自ノードと、自ノードの後をつぐ唯一の子の両方が黒の場合について考察します。
削除によって、この部分の黒の段数が1減るため、バランスの調整が必要となります。
自ノードを置き換える唯一の子を N、
N の新しい親(消えた自ノードの親)を P、
N の新しい兄弟(P のもう一人の子)を S 、
S の左部分木を SL 、
右部分木を SR と表すことにします。
繰り返しますが、以下 N は黒です。
【削除 ケース1】
N が根の場合、調整完了です。 自ノードが黒でしたから、黒で置き換わることによって、
左右の黒の段数が1減った状態で条件が成立しています。
以下のケースでは P が存在します。
したがって、 NIL(黒)の場合を含めて S が存在します。
【削除 ケース2】
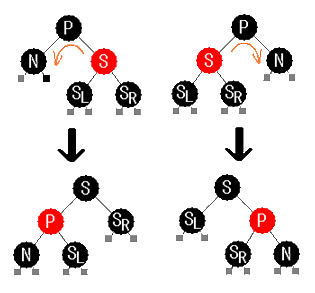
S が赤の場合
S が赤ですから、P 、 SL 、 SR は黒です。
この場合、 P を中心に外側にローテーションし、 S と P の色を反転します。
関連する全てのノードで黒の段数が変わっていませんから、N のノードで1減ったままということになります。
N 2
P 1
S 1
SL 2
SR 2
P が赤、
S が黒になりましたから、ケース4〜6に帰着されました。
左側の場合
SL を
S に、
右側の場合
SR を
S にして色の調整を進めます。
新しい
S の下がどうなっているかで、ケース4〜6に分かれて行きます。
以下、S が黒の場合です。
P 、SL 、SR の赤黒の組み合わせが残っています。
SL と SR が共に黒のケースをまずケース3、ケース4とします。
【削除 ケース3】
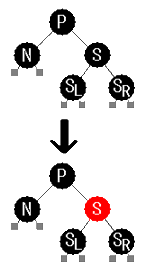 P が黒、SL が黒、SR が黒の場合。
P が黒、SL が黒、SR が黒の場合。
S を赤に変えます。
これにより、
S 、 SL 、SR の黒の階層が1減り、
P の左右のバランスが回復しました。
P の黒の深さが1減少しましたので、
P を新たな N として再帰的に色の調整を進めます。
このケースは最悪根まで伝播し、ケース1で終了します。
【削除 ケース4】
P が赤、SL が黒、SR が黒の場合。

P を黒に、S を赤に変えます。
これにより、
P の右部分木の黒の深さを変えることなしに、
P の左部分木の黒の深さを1増やすことができました。
以下のケースは、 P の色は赤でも黒でもかまいません。
【削除 ケース5】
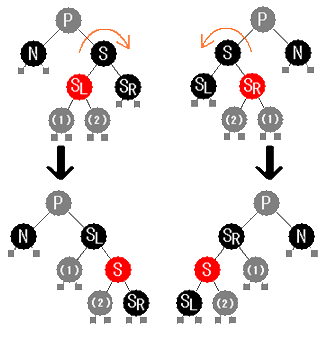
SL が赤、SR が黒、N が P の左の子 の場合および、
SL が黒、SR が赤、N が P の右の子 の場合。
言い替えると、S の子のうち内側の子が赤の場合、
S を中心に外側にローテーションし、
S を赤に変更し、
赤だったSL または SR を黒に変更します。
これにより、全てのノードの黒の深さを変えずにケース6の帰着しています。
【削除 ケース6】
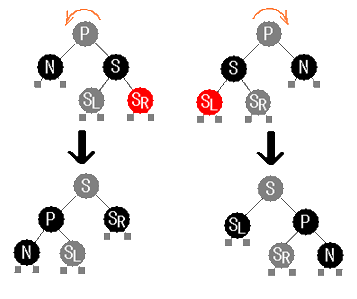 SR が赤、N が P の左の子 の場合および、
SR が赤、N が P の左の子 の場合および、
SL が赤、N が P の右の子 の場合。
言い替えると、 S の外側の子が赤の場合、
P を中心に N の側にローテーションし、
P と S の色を交換し、
赤だった SR または SL を黒にします。
これにより、SR と SL の黒の深さを変えずに、
N の黒の深さを1増やすことができました。
P と S について黒の深さが入れ替わりましたが、
ローテーションを行った部分木の上から見た黒の深さが変わっていませんから、
条件5の調整は完了です。
新しく一番上にきた S の色は、元々ここにあった P と同じ色ですから、
条件4も大丈夫です。
色の調整が再帰的に根に向かって進むケース3以外は、
最高3回のローテーション(ケース2 → ケース5 → ケース6)で調整が終わります。
【プログラム】
上記の【挿入アルゴリズム】と【削除アルゴリズム】のケース分けを網羅した単体試験を行いました。
ケースごとの試験データは insert メソッドでノードのパターンを作成し、
色の組み合わせを手動で設定しました。
完全な試験にするには、色の組み合わせも含めて insert で作成するのが理想ですが、
時間の節約をしました。
確認項目は、挿入・削除後のおもなノードの位置の確認および、
色については変更された全ての色の確認をおこなっています。
テストプログラム RedBlackTreeTester.java
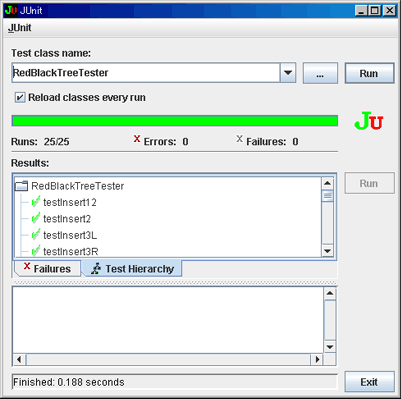
実行と結果
JUniit については、
テスティングフレームワーク JUnit
を参考にしました。
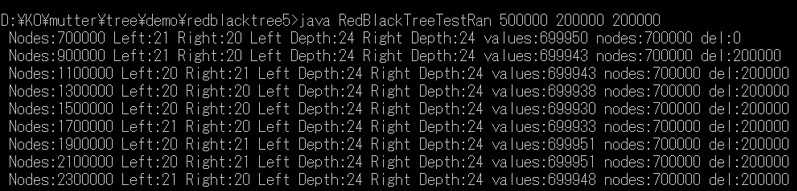
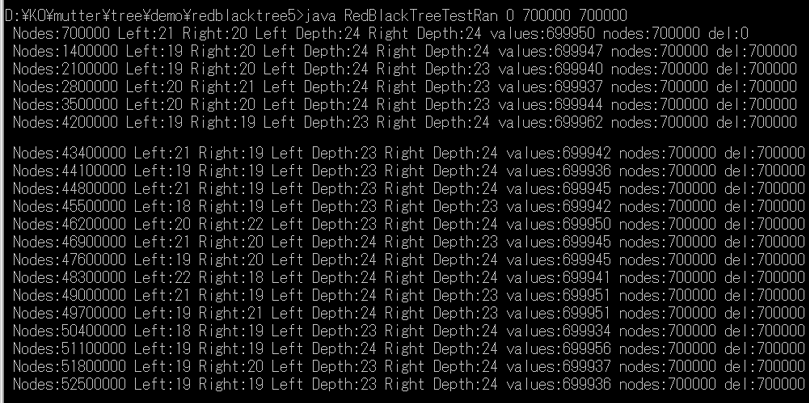
【負荷試験】


 赤のノードを挿入したのですから、
赤のノードを挿入したのですから、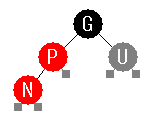



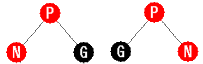
 以下、削除される自ノードと、自ノードの後をつぐ唯一の子の両方が黒の場合について考察します。
削除によって、この部分の黒の段数が1減るため、バランスの調整が必要となります。
以下、削除される自ノードと、自ノードの後をつぐ唯一の子の両方が黒の場合について考察します。
削除によって、この部分の黒の段数が1減るため、バランスの調整が必要となります。

 P が黒、SL が黒、SR が黒の場合。
P が黒、SL が黒、SR が黒の場合。


 SR が赤、N が P の左の子 の場合および、
SR が赤、N が P の左の子 の場合および、